The Project in a Few Words
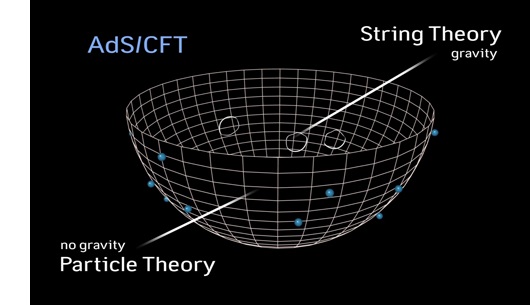
The Holographic duality is a non-trivial connection between gravitational theories in asymptotically AdS spaces and conformal field theories defined on the AdS boundary. As a weak-strong duality it allows the performance of calculations in the strongly-coupled regime of both theories with the use of perturbative calculations in the weakly coupled regime of the other theory.
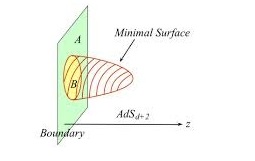
Several interesting quantum phenomena in the dual CFT are characterized by a fundamental quantum behaviour widely known as quantum entanglement. When a composite quantum system lies in an entangled state, the measurements in one subsystem are correlated to measurements in its complementary subsystem in such a way that there is no state description for either subsystem. The quantum entanglement is usually quantified via the measure of Entanglement Entropy. The latter has a nice geometric interpretation in the framework of the holographic diality: let the entangling surface be a closed surface at the boundary separating the degrees of freedom of the CFT to two subsystems; then the corresponding entanglement entropy is proportional to the area of the open minimal surface in the bulk geometry that it is anchored at the entangling surface in the boundary.
The specification of such minimal surfaces is in general a difficult task. Minimal surfaces in AdS4 are described by a Euclidean Non-linear Sigma Model (NLSM) defined in a symmetric target space, which is in turn reducible to the cosh-Gordon equation. The inversion of solutions of the cosh-Gordon equation to solutions of the initial NLSM is highly non-trivial. A recent development allows the inversion of a specific class of such solutions that can be expressed in terms of elliptic functions (Eur. Phys. J. C77 no.11, 797). The main goal of the proposed work is the extension of these techniques towards the discovery of new minimal surfaces in hyperbolic spaces corresponding to kinks on a constant energy density background in the reduced integrable system. Then, these new surfaces will be used in a twofold direction:
Main Goal 1
The verification of the equivalence of the first law of entanglement thermodynamics in the boundary theory to the linearized Einstein equations in the bulk side, and, thus, a better understanding of gravity as an entropic force emerging from the quantum entanglement statistics of the boundary CFT.
Main Goal 2
The expression of the renormalization group flow of entanglement entropy as a geometric flow, the study of the dependence of entanglement entropy on the entangling surface geometric characteristics and the use of the above tools for the study of strongly coupled quantum systems, such as superconductors.
Facts
The program supports
Post-doctoral Researchers
for
Months
The project is funded by the Hellenic Foundation for Research and Innovation
and the General Secretariat for Reasearch and Technology.
The project is based in the Institute of Nuclear and Particle Physics
of the National Centre for Scientific Research "Demokritos".
The Physics
Strongly Coupled Systems and Duality
Modern physics is full of strongly coupled systems of great interest not only from a theoretical point of view, but also in terms of potential applications. Such systems have extremely difficult mathematical calculability since perturbative techniques fail to describe the strongly coupled regimes of such dynamical systems, and, thus to capture the essential underlying dynamics. Such problems appear in a wide range of applied fields such as Hydrodynamics, Plasma Physics and Condensed Matter Physics (High-Temperature Superconductors, Superfluidity, Quark-Gluon Plasma Physics). Furthermore, such problems appear in conceptual problems of High Energy Physics such as Confinement, Black Hole Physics and Quantum Gravity.
A modern approach to the description of strongly coupled system is the use of dualities. Such tools are not available for any strongly-coupled system; nevertheless, when they exist, they comprise very powerful calculational tools. A duality is a non-trivial connection between two theories, that do not necessarily share many common characteristics, and which maps the weakly-coupled regime of one theory to the strongly-coupled regime of the other and vice versa. Such non-trivial connections are known to exist in the case of supersymmetric gauge theories. The formal proof of a duality is by construction elusive, as it is equivalent to the full solution of the strongly-coupled regimes of the two theories, which furthermore would render the duality useless. Even though, the existence of a duality can be supported via the calculation of certain quantities that are calculable due to the existence of special symmetries, i.e. supersymmetry, which protects them in the strongly coupled regime.
The establishment of a duality enables the performance of non-trivial calculations in the non-perturbative regime of one theory performing perturbative calculations in the dual theory. A prototype paradigm is the Seiberg-Witten duality in N=2 supersymmetric non-abelian gauge theories (Nucl. Phys. B 426, 19). A major outcome of this program is the qualitative understanding of confinement, in this class of theories, as the condensation of non-perturbative magnetically charged particles effectively leading the system to a "magnetic superconductor" phase. In this phase the electric fields are scattered off by the analogous of Meissner effect, enforcing charged objects in the theory to form bound states with vanishing electric color charge, similar to the mesons and baryons in Quantum Chromodynamics.
The Holographic Duality
A massive development in the study of strongly-coupled systems via the use of dualities is the use of holographic dualities that followed the original formulation of the AdS/CFT correspondence (Int. J. Theor. Phys. 38). The AdS/CFT correspondence is a broad framework that relates (d+1)-dimensional gravitational theories in asymptotically Anti-de Sitter space-time to d-dimensional non-gravitational conformal field theories. Since conformal field theories describe systems near critical points, either quantum mechanically or thermodynamically, the holographic duality has found applications in many physical systems. Furthermore, it provides a non-perturbative formulation of string theory and it is the most successful realization of the holographic principle, an idea in quantum gravity originally proposed by Gerard 't Hooft and promoted by Leonard Susskind.
One of the first applications of the duality was in the context of Quark Gluon Plasma and its Hydrodynamics (Phys. Rev. Lett. 87, 081601). Via the holographic duality, simple calculations in the gravitational theory allow the specification of an upper bound for the ratio of viscosity over entropy density, for fluids that are described by a conformal field theory. None of the known fluids violates this bound and experiments at RHIC suggest that quark-gluon plasma approaches but it does not violate this bound (Phys. Rev. C 78, 034915). The program of studying strongly coupled systems in condensed matter physics through the holographic duality has advanced a lot ever since, allowing the description of quantum phases of matter such as superconductivity (Phys. Rev. Lett. 101, 031601) and superfluidity (Phys.Rev. D 79, 066002), as well as the relevant phase transitions.
The holographic duality has been proven equally effective in the converse direction, too, allowing the calculation of observables in quantum gravity from the conformal field theory side. In this sense, the conformal field theory may serve as the non-perturbative definition of string theory in AdS space-times. Such calculations allow the resolution of many fundamental questions on quantum gravity, such as the information paradox. The latter, stated by Hawking long ago, questions the unitarity of quantum gravity since in the semi-classical approximation, black holes appear to destroy information, as they evaporate emitting thermal radiation. This radiation does not contain the information which was gathered in the interior of the black whole during its lifetime, thus, information seems to be destroyed. This paradox is absent in the conformal field theory side and the use of the holographic duality has provided tools towards the understanding of the resolution of this paradox in the gravity side (JHEP 1310, 212).
Quantum Entanglement
Quantum Entanglement is a fundamental quantum behavior, without classical analogue, that emerges in complex quantum systems that are either constructed or interact in such a way that the state of any subsystem is not independent of the state of the other subsystems. In such cases, only a state of the overall system can be properly defined. In the presence of quantum entanglement, observables of the entangled subsystems are correlated, even when the measurements are space-like separated. This led to the formulation of the famous Einstein-Podolsky-Rosen (ERP) Paradox (Phys. Rev. 47, 777). Initially, such behavior was considered as violating local causality and served as an argument in favor of a hidden variables interpretation of quantum mechanics, however, it was experimentally verified (Phys. Rev. D, 10 526-35)] in spin and polarization measurements of entangled particles.
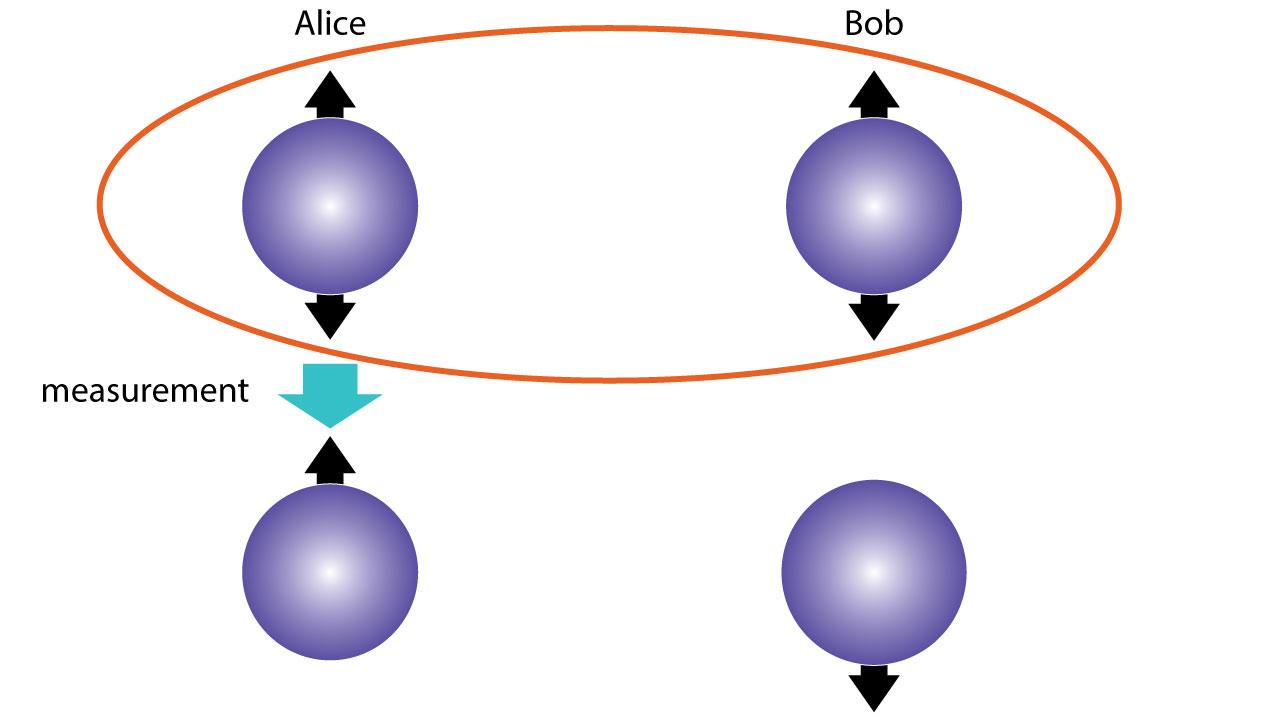
Quantum entanglement is vital in the quantum information science, in applications that are already available such as quantum teleportation (Phys. Rev. Lett. 70, 1895-1899) or quantum cryptography. Furthermore, quantum entanglement is crucial in the development of the very promising application of the quantum computers (Journal of statistical physics. 22 (5): 563-591), since most quantum algorithms, like the Shor factorization algorithm (SIAM J.Sci.Statist.Comput. 26 (1997) 1484), take advantage of quantum entanglement in order to succeed much faster solutions of mathematical problems in comparison to the classical algorithms.
The study of the consequences of quantum entanglement in diverse physical phenomena requires the introduction of quantitative measures. The most common measure used in bibliography is the entanglement entropy. When a complex quantum system is in an entangled state, the reduced density matrix that describes a particular subsystem A corresponds to a mixed state. The more entangled the total system is, the more dispersed is the spectrum of the reduced density matrix. As a consequence von Neumann entropy, defined on the spectrum of the reduced density matrix, is a good measure of quantum entanglement. This quantity is defined as the Entanglement Entropy (SEE)
SEE = tr(ρAlnρA), where ρA = trBρ,
where ρ is the density matrix of the overall system and B is the complementary of subsystem A. The entanglement entropy is used in a wide range of applications, such as the study of quantum phases in Condensed Matter Physics, where it allows the identification of topological phases and the characterization of critical points (Phys. Rev. Lett. 96, 110404, Int. J. Quant. Inf. 4, 429).
Entanglement in Holography
Many strongly coupled phenomena that one tries to approach through the Holographic Duality, i.e. superconductivity, are of purely quantum nature. Such phenomena are strongly characterized by the existence of quantum entanglement. Therefore, the study of such systems through the holographic duality requires the interpretation of some measure of entanglement in the side of the gravitational theory.
Recently in the context of Holographic Duality, it has been proposed that quantum entanglement is related to the quantum structure of space-time and that entanglement entropy in particular is the appropriate measure that quantifies the relation between geometry and quantum entanglement (Phys. Rev. Lett. 96 181602). This conjecture, named after Ryu and Takayanagi, provides a quantitative tool for the understanding of strongly coupled systems using the holographic duality. More specifically, the Ryu-Takayanagi conjecture suggests that the entanglement entropy, defined for a particular entangling surface that divides the boundary CFT degrees of freedom to two subsystems is directly related to the area of an open minimal hypersurface (Aextr) that lies in the bulk AdS geometry, whose boundary is the entangling surface.
The Ryu-Takayanagi conjecture enables the calculation of the entanglement entropy of strongly coupled systems, through simple calculations on the gravity side of the theory (JHEP 1105, 036). Such calculations are extremely interesting from the point of view of condensed matter physics, since they provide information about properties of strongly coupled systems. Similarly, these results can be used in order to obtain bounds on the dynamical parameters of the gravitational theory (PoS CORFU 2014, 157).
A major achievement of the Ryu-Takayanagi conjecture is the reproduction of an "area law", which emerges in many aspects of Quantum Gravity, such as the entropy of black holes, or the Bekenstein bound. In this context, quantum entanglement serves as a natural mechanism for this kind of behavior. The interactions in quantum many-body systems are local. The locality of the interactions is imprinted in the dependence of entanglement entropy on the size of the subsystem under study. When the overall system lies at the ground state, entanglement entropy scales with the area of the boundary separating the subsystem from its environment, rather than its volume (Phys.Rev.Lett. 71 666-669).
The similarity between the laws of black holes physics and laws of thermodynamics is known since long ago. This similarity indicates the existence of a profound relation among gravity and thermodynamics (Commun. Math. Phys. 31 161). In this spirit, there have been many efforts towards the understanding of Einstein Equations as thermodynamic equations describing some underlying degrees of freedom (Phys. Rev. Lett. 75 (1995) 1260). The Ruy-Takayanagi conjecture motivates the relation of quantum gravity with thermodynamics, but in a radical different way. Gravity in this picture is an entropic force, but it is connected to quantum statistics related to quantum entanglement and not to thermal statistics.
In particular, the appropriate thermodynamic relation is the so called "first law of entanglement thermodynamics", which is a trivial statement for any quantum system. It states that in the case of small variations of the state of the overall system, the variation of entanglement entropy is equal to the variation of the expected value of the modular Hamiltonian, which is defined as the logarithm of the reduced density matrix. In the dictionary of the AdS/CFT correspondence, small variations of the state of the total system are mapped to small perturbations of the geometry in the gravitational side. Even though the Ryu-Takayanagi conjecture is a rather simple statement, the actual calculation is highly non-trivial for both the variation of entanglement entropy and the expectation value of the modular Hamiltonian in the gravitational side. However, in the very special case of spherical entangling surfaces, both quantities can be calculated analytically. Imposing the first law of thermodynamic entanglement turns out to be equivalent with the requirement that the small perturbations of the geometry should obey the Einstein equations at linear level (J. High Energy Phys. 1404 195). The original results were obtained for metric perturbations subject to Dirichlet boundary conditions and later, in the case of AdS4 they were generalized for variations that are subject to more general boundary conditions (Nucl.Phys. B 896, 440).
The Ruy-Takayanagi conjecture can also be directly applied in the case of non-connected entangling surfaces. In this case there is more than one "competing" minimal surfaces that are appropriately anchored to the same entangling surface (Phys. Rev. D 82 126010). The visualization of this situation is easier if two separate compact entangling regions are considered. In this setup, there are two minimal surfaces, one comprises of the union of the minimal surfaces that correspond to each separate entangling surface and another one having the form of a tube that connects the two entangling surfaces. The question about which surface corresponds to the global minimum is dependent on the spatial separation and the size of the entangling surfaces. The fact that the global minimum depends on values of parameters indicates the existence of a geometric phase transition. This behavior is exhibited in lattice simulations of SU(N) gauge theories and it is related to confinement. Such holographic calculations have been conducted mostly in 3-dimensional space-time. As a result the boundary is one-dimensional, meaning that the entangling surfaces are simply points that define some line segments. Similar calculations in higher dimensional cases have to face the challenge of finding the minimal surface that corresponds to a more general entangling surface than a spherical one.
At the Frontier and Beyond
One of the major obstacles in the application of the Ryu-Takayanagi conjecture is the analytic specification of the minimal surfaces that correspond to an arbitrary entangling surface. The associated equations are non-linear and therefore, they can be solved only in the case of very special geometries. The great majority of the literature is based on entangling surfaces that are either spherical or infinite stripes. In both cases the entangling surface has a trivial geometry; it is characterized by either constant or vanishing curvature. The study of minimal surfaces for more general entangling surfaces exhibits great interest; apart from the purely mathematical interest, such calculations can be an important step towards the understanding of the dependence of the area of the minimal surface (and equivalently of entanglement entropy) on geometric properties of the entangling surface, such as the curvature or singular non-smooth points. Such generalizations of minimal surfaces, if they also include cases that correspond to non-connected entangling surfaces too, may lead to the study of geometric phase transitions, which are related to the physics of confinement in gauge theories.
The Structure of our Project
Our project is comprised of 5 research work packages and 1 more dedicated to the publication and dissemination of the results
WP1: Dressed Minimal Surfaces in AdS4
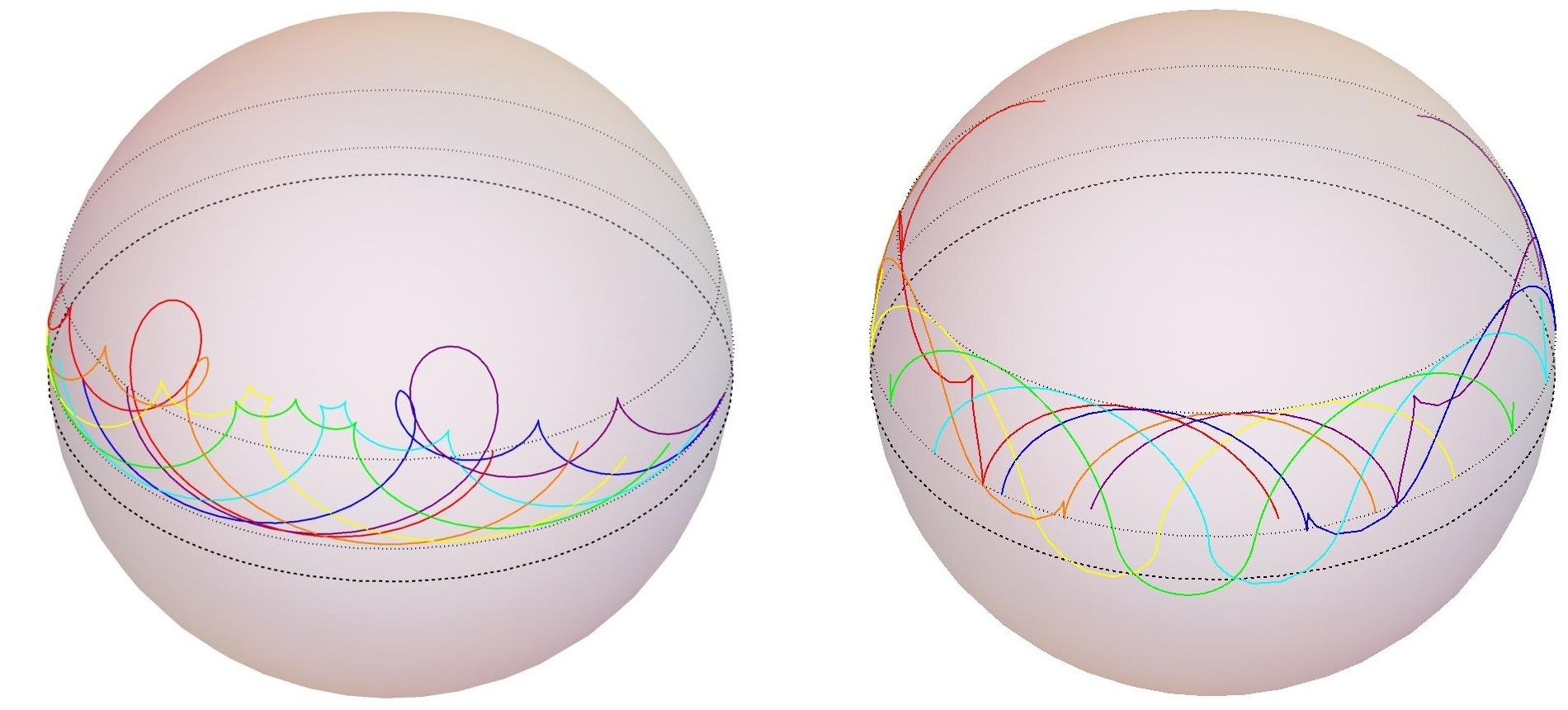
It is long known that two-dimensional Non-Linear Sigma Models (NLSMs), defined on symmetric spaces, can be reduced to integrable systems that belong to the family of the sine-Gordon equation. This reduction is known as Pohlmeyer reduction. More specifically in the case of AdS4, Pohlmeyer reduction maps static minimal surfaces to solutions of the Euclidean cosh-Gordon equation. The mapping of the degrees of freedom of the NLSM to those of the reduced system is non-local; therefore, the inversion of the process is highly non-trivial. Recently (JHEP 1607 070), a new approach was established, which is capable to invert the Pohlmeyer reduction for elliptic solutions of the integrable model. Key element of the approach is the relation between the NLSM solutions and the band structure of the exact solvable periodic Lame potential.
It is also well known that the integrable systems of the family of the sine-Gordon equation possess transformation, the so called Backlund transformations, which allow the specification of a new solution from a given one, solving only first order differential equations instead of second order ones. Such solutions cannot be inverted to minimal surface solutions with the use of techniques of (JHEP 1607 070). However, this will be achieved with the dressing method (Commun. Math. Phys. 92, 329), which is the equivalent of the Backlund transformations in the language of the Non-linear Sigma Model (JHEP 0904, 060). It has to be noted that the difficulty of the application of the dressing method on an elliptic minimal surface background is expected to be significantly increased in comparison to the usual applications of the technique in the field of classical string solutions (JHEP 0610, 012). In such cases, the dressing method is applied on an NLSM solution corresponding to the vacuum of the reduced system, resulting to NLSM solutions corresponding to kink or breather solutions of the reduced system. However, in the case of minimal surfaces, the reduced system is the cosh-Gordon equation, which lacks a vacuum solution, and, thus, the application of the dressing method to more complicated seed solutions is the only choice.
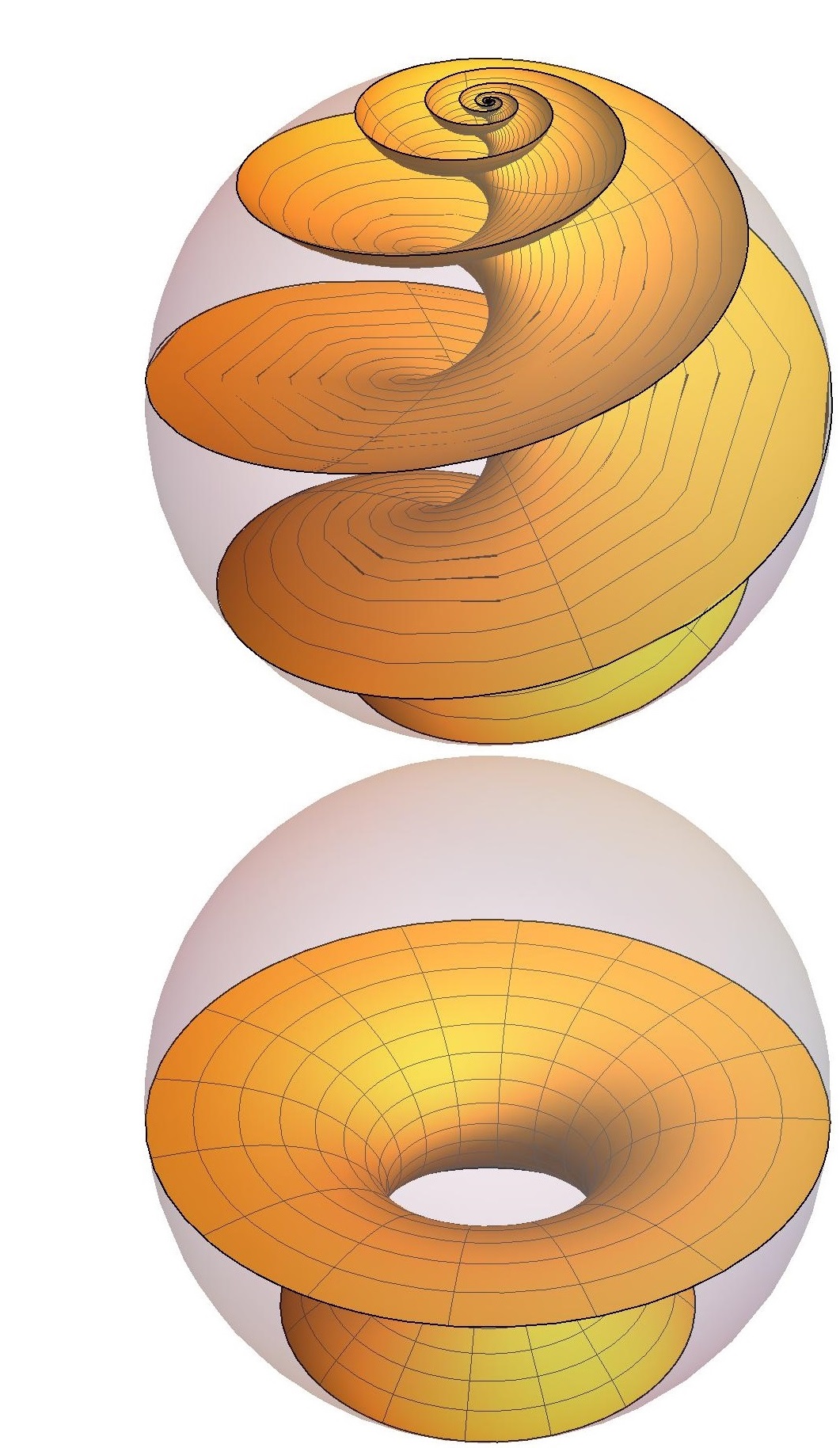
The application of the dressing method will produce a tower of new solutions from each known elliptic minimal surface, significantly enlarging the set of available tools for verification checks of the Ryu-Takayanagi conjecture and the study of gravity as a quantum entropic force. These solutions will be studied in terms of global and local stability. Furthermore possible geometric phase transitions between them and applications in the description of confinement will be studied. Finally, the dependence of their area to the form of the entangling surface and on a radial cutoff will be studied to facilitate the following work packages.
WP1a: Dressed Elliptic Classical String Solutions
The results of WP1 have a direct generalization to classical string solutions in AdS backgrounds of the form of (JHEP 1607 070) or in other symmetric spaces such as the sphere. In this side work package, the methods of work package 1 will be applied to these cases to derive new classical string solutions, the related dispersion relations and probe the holographic duality in the strong-coupling limit of the boundary CFT. The new solutions are also expected to expose several interesting properties of the string dynamics on symmetric spacetimes, which are absent in the simple case of elliptic solutions, such as spike interactions and instabilities.
WP2: Entanglement Entropy in Field Theory
In order to compare the dependence of the entanglement entropy on the energy cutoff with the field theory prediction, the methods of (Phys.Rev.Lett. 71 666-669) will be used in order to calculate the entanglement entropy on the field theory side. More specifically, the dependence of the entanglement entropy on the geometry of the entangling surface and the cutoff scale must be specified. These techniques are well suited for this application since discretization of the space coordinates applied in (Phys.Rev.Lett. 71 666-669) is directly equivalent to the introduction of an energy cutoff. The methods of (Phys.Rev.Lett. 71 666-669) should be expanded in order to treat more general states than the ground state of the system and in particular thermal states. In addition discretization should be applied to all spatial directions, not only on the radial one, as in the original paper.
The main goal of WP2 is the study of the dependence of entanglement entropy on the geometric characteristics of the entangling surface, i.e. curvature and the existence of non-smooth points, and the energy cutoff scale, using techniques similar to those of (Phys.Rev.Lett. 71 666-669). Furthermore the scaling properties of entanglement entropy with the size of the considered subsystem are going to be investigated and compared with the usual "area law" dependence. The main system under study will be free field theory in the ground state and in a thermal state, but if time is available extensions to interacting field theories will be investigated. The output of this work package will act as an essential input and validity check for WP3.
WP3: Holographic Renormalization of Entanglement Entropy
In the framework of holographic theories it is understood that the radial coordinate of AdS is related to the energy scale in the boundary field theory. Therefore, the introduction of a radial cutoff at minimal surfaces in AdS, corresponds through the Ryu-Takayanagi conjecture, to the insertion of an energy scale cutoff in the calculation of entanglement entropy in the field theory. This picture is in perfect agreement with the expected dependence of entanglement entropy on the energy cutoff. The relation between the radial cutoff and the area of minimal surface is obviously strictly increasing, while the area tends to zero at a finite value of the radial cutoff. This fact is in line with the physics of entanglement on field theories. In particular, the reduced density matrix of the subsystem for a given entangling surface, in general describes a mixed state which is a superposition (classical and quantum) of all eigenstates of the subsystem, even if the overall system lies at its ground state. The introduction of an energy scale cutoff in the field theory forces the reduced density matrix to be defined in a subset of these eigenfunctions. As a result, lowering the cutoff shrinks the subset altering the spectrum of the reduced density matrix and making it approach the density matrix of a pure state, enforcing the entanglement entropy to decrease. Finally, setting the cutoff below the first excited state of the subsystem, forces the subsystem to lie at its ground state, thus the entanglement entropy should vanish at a finite energy cutoff.
The above indicate that Ryu-Takayanagi conjecture can provide a framework for the description of the renormalization group flow of the entanglement entropy, through the understanding of the dependence of the shape of minimal surfaces on the radial AdS coordinate. The calculation of the entanglement entropy RG flow is of direct interest for the description of strongly correlated systems of condensed matter physics and the relevant phase transitions.
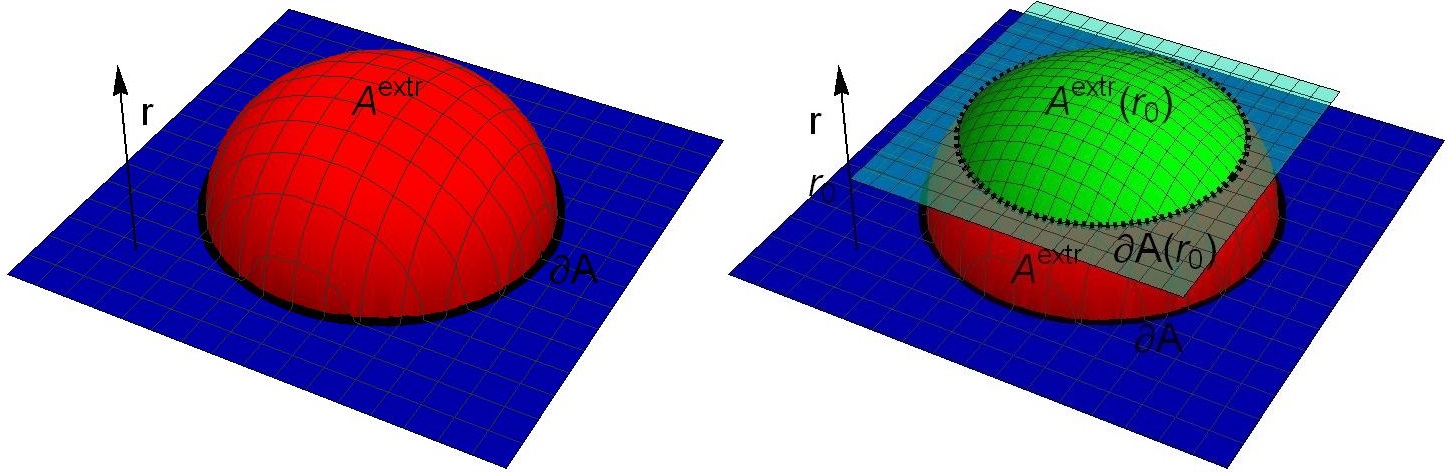
The availability of new minimal surfaces with non-trivial geometric characteristic will allow the study of the dependence of the form of minimal surface on the radial coordinate. For this purpose, the embedding of a minimal surface inside the AdS will be studied, as well as the embedding of the intersection of the minimal surface with a constant radius surface, both in the constant radius surface and in the minimal surface. The combination of the above will enable the expression of the dependence of the metric geometry of the minimal surface on the radial coordinate as a geometric flow. Therefore the dependence of the entanglement entropy on the radial cutoff will be expressed as a geometric flow directly applicable to strongly coupled condensed matter systems.
The main goal of WP3 is the study of the dependence of the area of the elliptic minimal surfaces and those produced in WP1 from the radial cutoff. The minimal surfaces will be described as a geometric flow of the intersection of the minimal surface with a constant radius slice, resulting in a renormalization group flow equation for the entanglement entropy, revealing the dependence of the flow on the geometric characteristics of the entangling surface, such as its curvature or the possible existence of singular non-smooth points. Applications of the flow in the field of strongly-coupled systems of Condensed Matter Physics, such as superconductors and superfluids will be investigated.
WP4: Equivalence of First Law of Entanglement Thermodynamics and Linearized Einstein Equations
Finally, the equivalence of the first law of entanglement thermodynamics and Einstein equations has been verified in the case of spherical entangling surfaces. It has to be noted that such spherical surfaces are special in the sense that they are not just characterized by vanishing mean curvature, but both principal curvatures are vanishing; they are the equivalent of planes in hyperbolic space. This fact restricts the significance of the proof. If the origin of gravitational force is indeed entropic, due to quantum entanglement, a mathematical formulation should exist that can prove this equivalence for any entangling phase. Besides the difficulty in the calculation of the minimal surface for an arbitrary entangling surface, additional difficulty arises since the holographic analogue for the modular Hamiltonian is also unknown for an arbitrary entangling surface. The origin of the difficulty is the fact that the modular Hamiltonian is in general a non-local function of the holographic energy-momentum tensor. In certain special cases, like in the case of spherical entangling surfaces, the modular Hamiltonian generates a geometric flow that allows its expression as a local operator. The discovery of analytic expressions for the modular Hamiltonian would be of particular interest, both in the framework of holographic duality by itself, and for the check of the equivalence between the first law of thermodynamic entanglement and Einstein equations. Even approximate expressions, linear to the holographic energy momentum operator, would be enough in order to probe the above-mentioned equivalence. Such approximate expressions would be local since non-local contributions require the insertion of the energy momentum operator at two different positions at least, and, thus, they would be of higher order.
The main goal of WP4 is the use of the minimal elliptic surfaces derived in (Eur. Phys. J. C77 no.11, 797) as well as those derived in work package 1 for the verification of the equivalence of the first law of entanglement thermodynamics and the linearized Einstein equations. For this purpose the variation of the entanglement entropy by the introduction of a metric variation with the use of the aforementioned minimal surfaces will be calculated. Then, based on the results of work package 1 and (Eur. Phys. J. C77 no.11, 797), first order expressions for the modular Hamiltonian in terms of the holographic energy-momentum tensor for the entangling surfaces of the aforementioned minimal surfaces will be derived. The variation of the expected value of the modular Hamiltonian by the introduction of a metric perturbation will be derived and finally, the compatibility of the above variations with Einstein equations and the first law of entanglement thermodynamics will be checked.
WP5: Publication and Dissemination of Results
1. This website
2. Presentation of the results in international conferences
3. One-day meeting in NCSR Demokritos on the outcomes of the project
4. Talk for the general public on the outcomes of the project
The Outcome of our Work


Publications in International Scientific Journals-Conference Proceedings-Conference Presentations
- All
- Journal Articles
- Conference Proceedings
- Presentations
- Popularized
Research Team
Our research team is comprised by 4 post-doctoral researchers and the Director of Research in NCSR "Demokritos" Minos Axenides

Georgios Pastras
Principal Investigator Dr. Georgios Pastras was born in Patras, Greece in 1980. He received his BS in Physics from University of Patras in 2002 and he obtained his PhD in Physics from Harvard University in 2009. He has worked as a post-doctoral scientific collaborator in Ecole Polytechnique Federale de Lausanne, University of Patras, National Technical University of Athens and currently at the National Center for Scientific Research "Demokritos". He has conducted research on Spontaneous Metastable Supersymmetry Breaking, Little Higgs Models, Black Hole Thermodynamics, Tunneling Solutions in Quantum Field Theory, Entanglement in Quantum Field Theory, Holographic Entanglement Entropy, Non-linear Sigma models and Classical String Solutions. Between 2012 and 2014, he had a side-career in Engineering, focusing on Energy Efficiency of Manufacturing Processes, Modelling of Non-conventional Manufacturing Processes and Robotics. Dr. Georgios Pastras has taught in Harvard University for nine semesters as a teaching fellow. He has received the "Certicate of Distinction in Teaching" by the Derek Bok Center for Teaching and Learning twice and he has been awarded with the "Harold T. White Prize for Excellence in the Teaching of Physics" by the Physics Department. Finally, he has received research funding from the Greek State Scholarship Foundation (2017-2019) and the Hellenic Foundation for Research and Innovation (2019-).
Minos Axenides
Director of Research in NCSR "Demokritos" Dr. Minos Axenides was born in Larisa, Greece. He received his BS in Physics from Columbia University and his PhD from Harvard University. He is a director of research (researcher A) at the Institute of Nuclear and Particle Physics in the National Center for Scientific Research Demokritos and he is currently serving as the deputy director of the institute. He has authored more than 50 articles in Theoretical High Energy Physics. His research interests include Quantum Mechanics and Quantum Field Theory, Quantum Statistical Mechanics, Nonperturbative Configurations in QFT, Strings and M-Theories, Astroparticle Physics and Cosmology, Nonlinear Dynamics, Chaos and Complexity. His has supervised two PhD theses and two master theses and he is a referee at several international scientific journals including Physical Review Letters, Physical Review D and Nuclear Physics B. Finally, he has received the 3rd Annual Prize from the Gravity Research Foundation of Boston.
Ioannis Mitsoulas
Post-doctoral Researcher Dr. Ioannis Mitsoulas was born in Athens, Greece in 1983. He received his BS in Physics from University of Patras in 2007 and he obtained his PhD in Physics from National Technical Univeristy of Athens in 2019. He is currently a post-doctoral scientific collaborator at the Institute of Nuclear and Particle Physics in the National Center for Scientific Research "Demokritos". He has conducted research on Pohlmeyer Reduction and Classical String Theory Solutions, as well as Modified Theories of Gravity. Between 2014 and 2015, he was a member of the Theory Division of CERN, where he worked on Gauge Theories with Extended Supersymmetry. Dr. Ioannis Mitsoulas has worked as a teaching assistant at the National Technical Univeristy of Athens for several semesters. Finally, he was the recepient of the IKY-CERN scholarship for PhD students from the Greek State Scholarship Foundation (2014-2015).
George Linardopoulos
Post-doctoral Researcher Dr. George Linardopoulos is a post-doctoral researcher in Theoretical Physics. His research interests include string theory, quantum field theory and integrability in the context of the AdS/CFT correspondence. He is currently studying one-point functions in holographic defect conformal field theories.
Dimitrios Manolopoulos
Post-doctoral Researcher Dr. Dimitris Manolopoulos was born in Pirgos, Greece in 1981. He received his PhD in Applied Mathematics form King’s College University of London in 2012. He has worked as a post-doctoral scientific collaborator at the National and Kapodistrian University of Athens as a recipient of an “ARISTEIA” grant. He is currently a post-doctoral scientific collaborator at the Institute of Nuclear and Particle Physics in the National Center for Scientific Research "Demokritos". During his PhD he conducted research in Mathematical Physics by studying the mathematical aspects of 2D Conformal Field Theories with defects and their underlying mathematical structures which include representation theory, Lie algebras and Category theory. He has also conducted research in Theoretical Physics and in particular, Entanglement in Quantum Field Theory, Holographic Entanglement Entropy as well as Integrability in Non-abelian T-Duality in Wess-Zumino-Witten models. Dr. Manolopoulos has also taught for one semester as a teaching assistant at King’s College London.Contact
You may contact the principal investigator at
pastras [at] inp.demokritos.gr
Patr. Gregoriou E & 27 Neapoleos Str, 15341 Agia Paraskevi, GREECE






















